jCAE - Amibe

Amibe is the name of jCAE main mesher. It reads OpenCASCADE geometries (BRep, STEP and IGES) and produces 3D finite element surface meshes. It is designed to create very large meshes (hundreds of millions of triangles), and tries to mesh even if geometry is dirty.

Algorithm

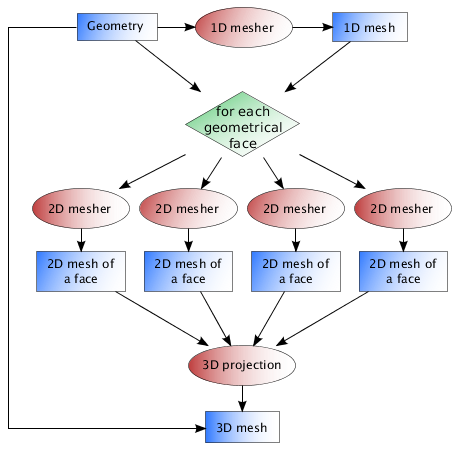
All edges are discretized first. This step is fast and does not need to be parallelized. Faces are then discretized, and edge discretization is not modified to ensure that final mesh is conformant. This is the most costful step, so it has been designed to run on clusters if needed. Each face can be meshed without interaction from other faces; there is no restriction on final mesh size, but in this step, each mesh of a face has to reside in memory. when finished, each mesh is written into separate files, and merged to produce final 3D mesh. Of course this step does not require loading whole mesh into memory!

Patch mesher

In OpenCASCADE faces are 2D parametrized surfaces. We mesh those parametrized surfaces so that the 3D projection on our geometry has the desired properties (edge length and/or deflection), as described in Maillage de surfaces paramétriques (in French), by Houman Borouchaki and Paul Louis George.

Background

1. Mesh files must be easy to parse with any language on any architecture.
2. Mesh may be huge (hundred millions of triangles) and handled by out-of-core algorithms.
3. A mesh is a set of nodes and triangles, but other data may be added (groups, results...), so the file format must be extendable.
4. There is no existing open file format designed to work with out-of-core algorithms, in both Java and native.

Format overview

XML is a convenient solution to store structured data, it is portable and our own file format can be easily designed and extended. But its main drawback is its verbosity and parsing an XML file containing several gigabytes would be challenging. We chose an intermediate solution: an XML file contains only structured data (link to geometry file, list of geometrical elements, etc) and raw data (like node coordinates) are stored into separate binary files.

1D, 2D and 3D meshes

Amibe creates 3 meshes in the same directory:

1. A discretization of geometrical edges. These are 1D linear elements (beams).
2. A 2D discretization geometry. These are 2D triangles. In order to help parallel computations, tessellation of different geometry patches are written into separate files.
3. A 3D discretization geometry. These are 3D triangles.

The two first meshes are intermediate steps to reach the third one which is the exploitable mesh for computation. Intermediate meshes are kept because they can be used in specific algorithms.

XML file

The exact format is given by a DTD (XML Schema format coming ASAP). The information it contains are:

• Path to binary files
• Number of nodes and triangles
• Path to geometry (only required for some algorithm)
• Description of groups and pointer in the binary group files

Binary files

• To ensure portability, binary files of amibe are always written in big endian.
• To make files easy to parse, they contains only one type of data (64 bit integer or double).
• Binary files do not contain any headers or meta data, they are only raw array.

1D binary files

An example of 1D XML file linking to these 1D binary files can be found here.

jcae1d.files/nodes1d.bin

1D node coordinates. All curves are concatenated, offset attribute tells at which position a curve is stored into binary file. File length is (sum of all number of nodes)*8.

jcae1d.files/nodes1dref.bin

References to geometrical vertices. We need to glue edge endpoints together when they are referring to the same geometrical vertex. An entry in this binary file consists of 2 integers:

• Node index in jcae1d.files/nodes1d.bin (starting to 1).
• Geometrical vertex number.

All curves are concatenated, offset attribute tells at which position a curve is stored into binary file. In practice, edge endpoints are geometrical vertices, and there is no other candidate, file length is thus 2*(number of geometrical edges)*2*4.

jcae1d.files/beams1d.bin

Beam tessellation. This file contains node index in jcae1d.files/nodes1d.bin (starting to 1) of segment endpoints. All curves are concatenated, offset attribute tells at which position a curve is stored into binary file. File length is (number of segments)*2*4.

2D binary files

An example of 2D XML file linking to these 2D binary files can be found here.

jcae2d.<patch_number>.files/nodes2d.bin

2D node coordinates. File length is (number of nodes)*8*2.

jcae2d.<patch_number>.files/nodes1dref.bin

References to 1D vertices. This is needed to glue patch boundaries. 2D vertices on different patches are assigned the same reference number if and only if they shared the same 1D ancestor. By convention, inner nodes are first written into jcae2d.<n>.files/nodes2d.bin, then boundary nodes are appended. This file contains an array of integers which are global reference numbers (and must be non-null). File length is (number of reference nodes)*4.

jcae2d.<patch_number>.files/triangles2d.bin

Patch tessellation. This file contains node index in jcae2d.<n>.files/nodes2d.bin (starting to 0) of triangles. File length is (number of triangles)*3*4.

3D binary files

An example of 3D XML file linking to these 3D binary files can be found here.

jcae3d.files/nodes3d.bin

3D node coordinates. File length is (number of nodes)*8*3.

jcae3d.files/nodes1dref.bin

References to 1D vertices. This may be needed if we want to preserve patch boundaries, this file has the same structure as in 2D. File length is (number of reference nodes)*4.

jcae3d.files/triangles3d.bin

Geometry tessellation. File length is (number of triangles)*3*4.

jcae3d.files/groups.bin

Groups. Each group contains the list of index (starting to 0) of triangles enclosed in this group. All groups are concatenated, offset attribute tells at which index (this is not position, it has to be multiplicated by 4!) a group is stored into binary file. File length is (total number of triangles)*4.

Examples

Here is how one can retrieve the 3D nodes coordinates of the 3rd triangle of the group named "foobar":

• Parse 3D XML root file into a DOM.
• Search the foobar node in the XML structure either with DOM API or XPath.
• Get the foobar group offset in the binary group file
• Seek the binary group file to offset+8 and get the triangle ID
• Seek the binary triangle file to triangle ID
• Get the 3 nodes ID
• Seek the binary node file to the 3 nodes ID

A Java code to do it will look like this:

Document document = parseXML("jcae3d");

//Open binary files
RandomAccessFile rafNodes = new RandomAccessFile(getNodeFile(document), "r");
RandomAccessFile rafTriangles = new RandomAccessFile(getTriaFile(document), "r");
RandomAccessFile rafGroups = new RandomAccessFile(getGrpFile(document), "r");

//Search the foobar node in the XML structure   
Element fooBar = getGroup(document, "foobar");

//Get the foobar group offset
long index = getGroupOffset(fooBar);

//Seek the binary group file to 4*index+2*4 and get the triangle ID
rafGroups.seek(4*index+8L);
int triangleID = rafGroups.readInt();

//Seek the binary triangle file to triangle ID
rafTriangles.seek(triangleID*3*4);

//Get the 3 nodes ID
int [] nodeIDs = new int[3];
for(int i=0; i<3; i++)
    nodeIDs[i] = rafTriangles.readInt();

for(int i=0; i<3; i++)
{
    rafNodes.seek(nodeIDs[i]*3*8);
    double x = rafNodes.readDouble();
    double y = rafNodes.readDouble();
    double z = rafNodes.readDouble();
    System.out.println(x+" "+y+" "+z);
}